Isospectral drums
In 1991, mathematicians Gordon, Webb, and Wolpert (Invent. Math. 110, pp 1–22) solved a famous problem posed by M. Kac: “Can one hear the shape of a drum?” That is, do the Dirichlet eigenvalues of a membrane determine the shape of the membrane? Their answer was “No!”, and they used a powerful mathematical technique to produce a counterexample, which in its simplest form is a pair of eight-sided nonconvex polygons. Gordon, Webb, and Wolpert also noted that a more elementary technique known as transplantation can be used to show that the spectrum of the Laplacian with Dirichlet conditions is the same for both regions. However, actually finding what the eigenvalues are is far more difficult; it’s essentially impossible to do analytically.
Wu, Sprung, and Martorell (Physical Review E , Jan 1995) were among the first to present the results of computations of modes for these shapes, but the accuracy of their results was not clear. Physicists Sridhar and Kudrolli at Northeastern University built microwave cavities in the shapes of the two polygons and determined 54 eigenvalues experimentally (Physical Review Letters, April 4, 1994,Science News, September 17, 1994). Their results were accurate only to about 0.1%.
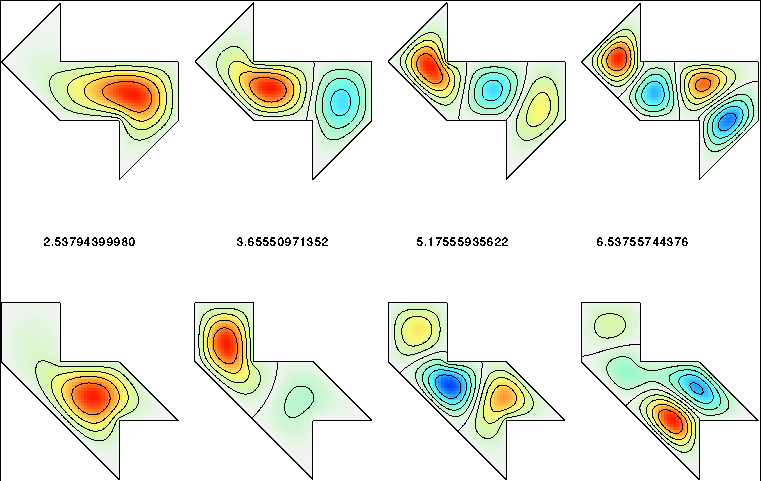
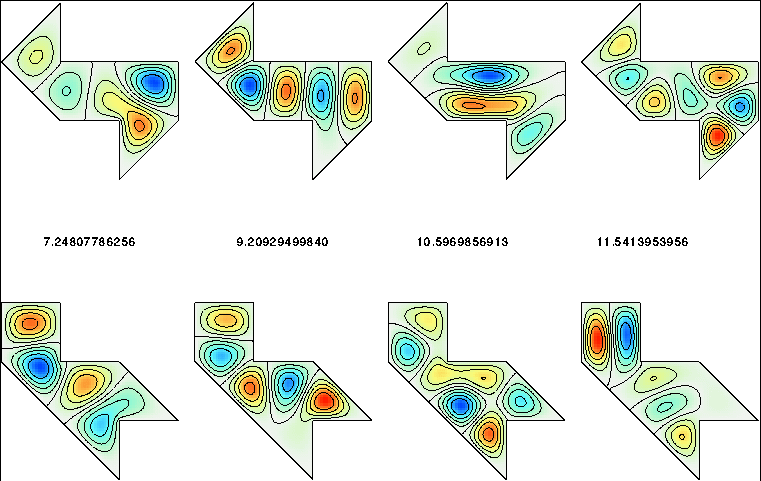
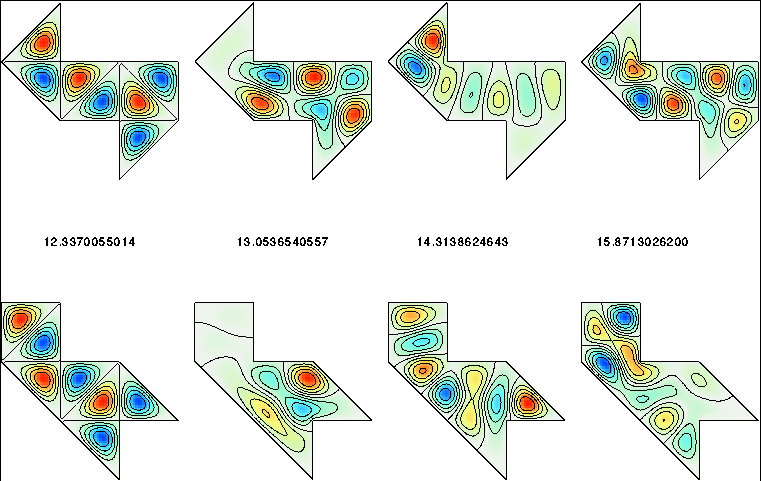
A little-known method due to Descloux and Tolley performed more accurately than all of these. The underlying principle is to exploit the well-known expansions of an eigenfunction near the corners. The criterion that selects eigenvalues is the matching of values and normal derivatives of the local expansions at interfaces within the polygons. Using this method in MATLAB, and incorporating a crucial improvement, in 1997 I published eigenvalues and modes 1–25 for both regions that were accurate to twelve digits.
One of the most basic uses of eigenmodes is to represent vibrations governed by the wave equation. Below are a few animations of such vibrations, based on different combinations of the first sixteen modes. Each movie runs for three periods of the first mode. (These don’t look great now, but they were made in 1995.)
The story of these and other isospectral shapes continued to develop from there, mathematically and computationally, but I was not much involved with most of it.